Certificat SSL - X509
X.509 est une norme spécifiant les formats pour les certificats à clé publique.
Un certificat SSL atteste l'identité d'une entreprise et est utilisé afin de chiffrer les données échangées sur un réseau.
Les certificats SSL sont soumis à la norme X509.
1.Présentation
Lors d'un échange HTTPS par exemple, les données sont chiffrés à l'aide du certificat.
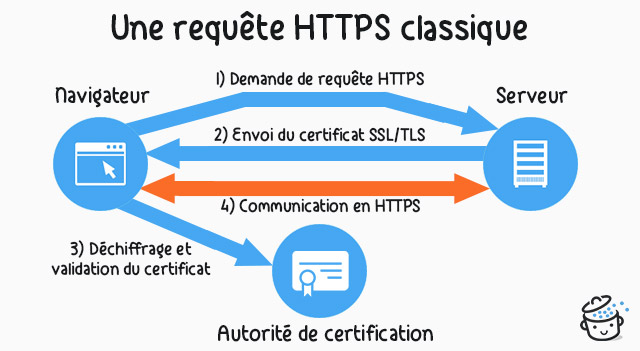
Si notre échange est intercepté par un attaquant , il est chiffré et donc incompréhensible.
Comme on peut le voir ci-dessus à l'initialisation de l'échange le certificat est envoyé en clair à travers le réseau.
2.Exploitation
Le but de l'exploitation est de recréer la clé privé qui a permis d'émettre le certificat(clé publique) pour pouvoir déchiffrer l'ensemble de la capture réseau.
2.1 Méthode 1 : Attaque par factorisation
Étape 1 : Extraction du certificat
Ouvrir la capture avec Wireshark (attention la version 1 semble avoir des problèmes)
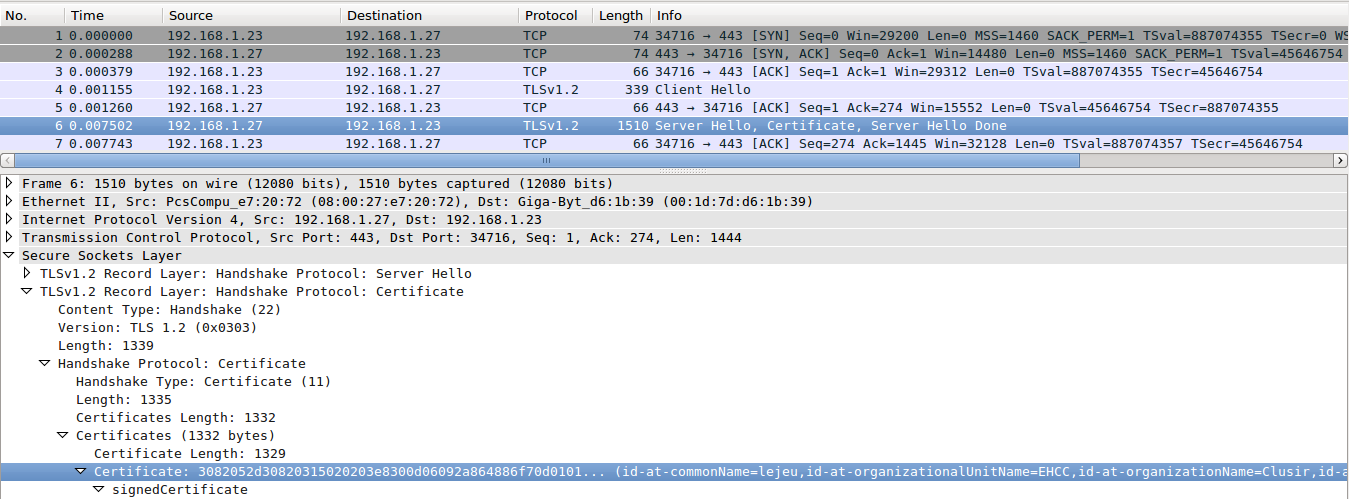
Sur le paquet 6 : “Server Hello , Certificate , Server Hello Done”
Dans la catégorie “Secure Socket Slayer” du paquet
On fait un clique droit sur “Certificate” ⇒ “Export selected packets bytes” et on enregistre en cert.der
Attention lors de l'extraction du certificat le fichier est bien en .der et non en pem
Étape 2 : convertir le .der en .pem
On utilise Openssl pour effectuer la conversion :
openssl x509 -inform der -in cert.der -out pubkey.pem
L'option :
- -inform : permet de stipuler le type de fichier donné en input
- -in : permet de donné le fichier en input
- -out : permet de donnée le nom du fichier de sortie
Il faut ensuite extraire le modulo de la clé publique :
openssl x509 -in pubkey.pem -text -modulus -noout
L'option :
- -text : permet d'afficher la sortie
- -modulus : permet d'afficher le modulo
Certificate:
Data:
Version: 1 (0x0)
Serial Number: 1000 (0x3e8)
Signature Algorithm: sha1WithRSAEncryption
[...]
Public Key Algorithm: rsaEncryption
Public-Key: (4096 bit)
Modulus:
00:86:98:65:48:c0:2b:2d:6b:04:61:a7:4a:09:a5:
[...]
Exponent: 65537 (0x10001)
Signature Algorithm: sha1WithRSAEncryption
31:17:4a:f4:96:40:0e:8d:56:f7:3f:46:1d:cf:0b:9d:25:5f:
[...]
Modulus=86986548C02B2D6B0461A74A09A5EE4EFA07882D5C610BDB14D1BA3044EFFD5570E4C509D116ACA992A342CF52ED0463DB6D4648A3013BA8219C3A72B1998796253DD11ECC536087E6E5BD207C1387AF9DF6BF875AB319556DCC0BAD6A90F017459760EE7D274FE6046E7599385F7607D29ED235477695E3365FC6B9F5270183E9C4C2C118AA676C1D9CBE06864507E4310D85B8CACFF9F5A3EED487B71D2D75B00943D7EDA9AAF5B2BB69271625DE2469D6A7C4F50C4EEAC54B1605793CC0F7FE9167452FF5FEF3647C9EEC8866730732C05DCA4C56F393CA2E61E7D76442822B9DA56D96F67BBA9F6095F761D0F2A3DE62EA8C6FC7AC2FA7B727684947F7640711B700F40A1799D0265EEFE94952B50E5E10B15BEC14CC1664714C6C1FF1C16454F4A912EC19760D80C4759FF3130DA43B13E7967D5CEA526402CF2B566653C0CD5D7D0995357661C0308CBD11AAEB832CA9093DC3981D1FB6B62FD98A883E8D4C1548521C3E2F0BEF76C7220D8093C2BDB1AE017F2E48D0DEFE42CE5713955AE294BEC2B5DA9B81CF9BB1D8CA5E5DCC9BF930EDB7A3F6D2D350D2AA478E01070DBC151D6F9F6DBA473EC001432DE4E2CED4611955F294B3D48631DD51EB7C50A97F5165731D597129D3335F4C994234D89095335C705F075A1BA08A0F5CF383D65CD424524A48A415CE2CA5A34B4287E4EFACB243E68B9C90A3679BEF2757
Il faut passer le modulo de l'hexa au décimal : ICI
On regarde si le modulo est connu sur factor-db :
http://factordb.com/index.php?query=549100898763808112064590568096509639806005267015788479836998648112330729762142760306265813195181231930171220686827142359040315653020182064933039077953579528749272321744478656324986362155106653831095037724728643255316641716947998245610175805278242802144980117927688674393383290354985820646326870614197414534217177211618710501438340081867982883181358830449072661742417246835970022211465130756382481343160426921258769780282358703413114522476037306476452786236456339806564839822630841425055758411765631749632457527073092742671445828538125416154242015006557099276782924659662805070769995499831691512789480191593818008294274869515824359702140052678892212293539574359134092465336347101950176544334845468112561615253963771393076343090247719105323352711194948081670662350809687853687199699436636944300210595489981211181100443706510898137733979941302306471697516217631493070094434891637922047009630278889176140288479340611479190580909389486067761958499091506601085734094801729179308537628951345012578144960250844126260353636619225347430788141190654302935255862518781845236444151680147886477815759103864509989480675169631226254252762579781553994364555800120817100328166428687776427164098803076677481602221304265962340500651339469391627432175447
Le modulo est entièrement factorisé sur le site , ces composantes sont disponibles.
On a donc :
e=65537 p = 2758599203 q= 199050626189790903113151725251371951406311367304411013359159100762029303668345459282823483508119186508070350039475140948570888009866572148405365532164833126992414461936781273087675274788769905198546175946505790118332257676994622928414648644875376193656132263418075334807302665038501361680530751104620475935886499714767992159620130246904875540624651891646715835632182355428589610236128648209568297096024509697960196858754170641081387466229916585122877955908862176165344465889280850859817985096316883025515924332365977538735425288433292357532172467247159245727072344354499113900733623716569924461327947462469348798798400461045817375922057805611166274339541877392159201774893120311667898551312256530117094221191204981071357303328506659872809131929265966688409379037586014938643190675726674943253875287765020503118408406103824607730713529079962656130622218633922911733000466212212532871890933508287965723844399784165195088175666883742686183165151553009638524764735387233844317375317153437534933611361683136151569588355535831475925641431859231311079029505004457816932257031352498323214304125608733640306746900473758755832661915903475867854937735150255829715879232213599597863424779218670961633567259935246911742292942052832671549 n= 549100898763808112064590568096509639806005267015788479836998648112330729762142760306265813195181231930171220686827142359040315653020182064933039077953579528749272321744478656324986362155106653831095037724728643255316641716947998245610175805278242802144980117927688674393383290354985820646326870614197414534217177211618710501438340081867982883181358830449072661742417246835970022211465130756382481343160426921258769780282358703413114522476037306476452786236456339806564839822630841425055758411765631749632457527073092742671445828538125416154242015006557099276782924659662805070769995499831691512789480191593818008294274869515824359702140052678892212293539574359134092465336347101950176544334845468112561615253963771393076343090247719105323352711194948081670662350809687853687199699436636944300210595489981211181100443706510898137733979941302306471697516217631493070094434891637922047009630278889176140288479340611479190580909389486067761958499091506601085734094801729179308537628951345012578144960250844126260353636619225347430788141190654302935255862518781845236444151680147886477815759103864509989480675169631226254252762579781553994364555800120817100328166428687776427164098803076677481602221304265962340500651339469391627432175447
Ici on remarque clairement le problème d'implémentation , p ne fait que 10 digits.
Étape 3 : Reconstruire la clé privé
On reconstruit la clé privé avec rsatool
python rsatool.py -n <n> -p <p> -q <q> -e <e> -v PEM -o privkey.pem
Étape 4 : Déchiffrer la capture
Pour ce faire il faut aller dans “Edition” ⇒ Préférences ⇒ Protocols ⇒ SSL
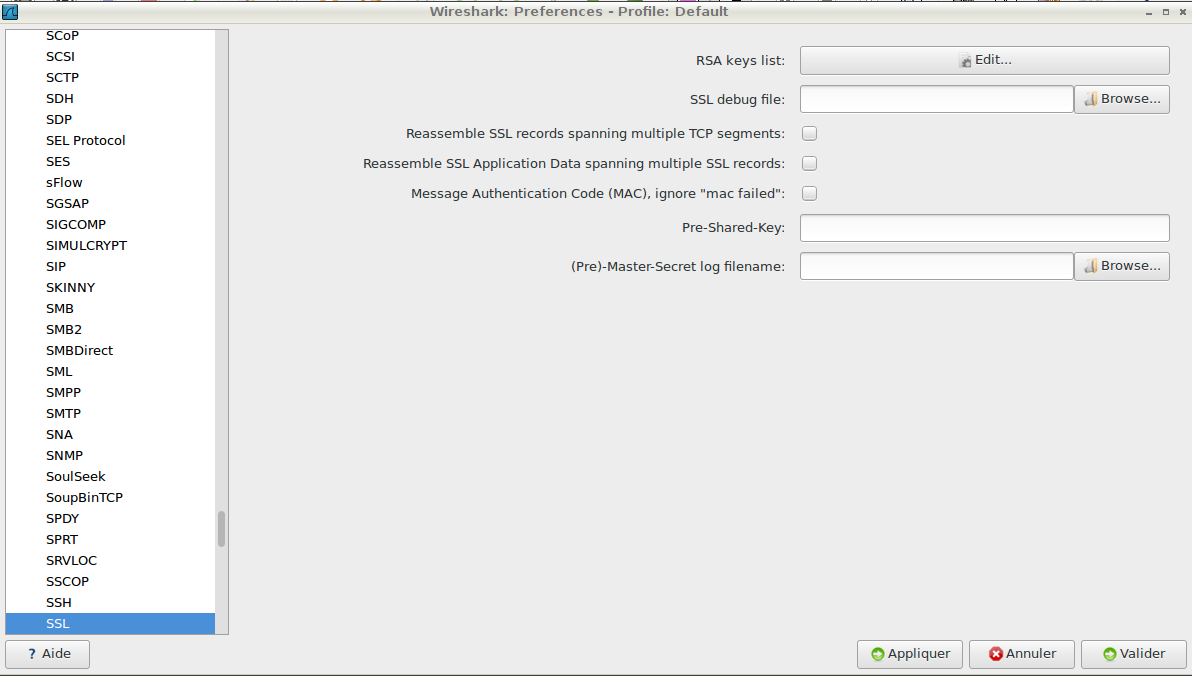
On ajoute une nouvelle clé dans “RSA Keys Lists”.
On remplit les champs comme ceci :
ip adresse : 192.168.1.27 port : 443 Protocol : http et on met notre fichier keypriv.pem
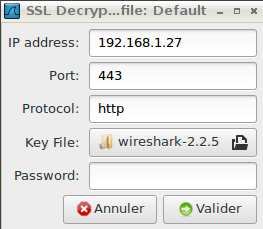
Une fois que c'est fait on obtient :
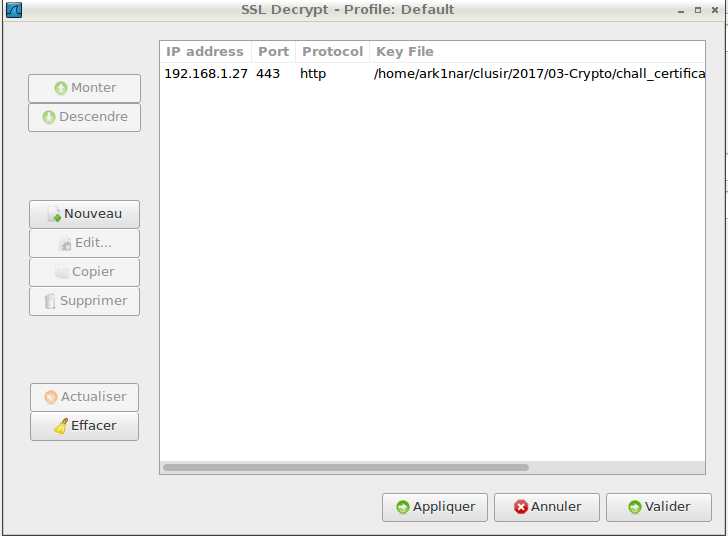
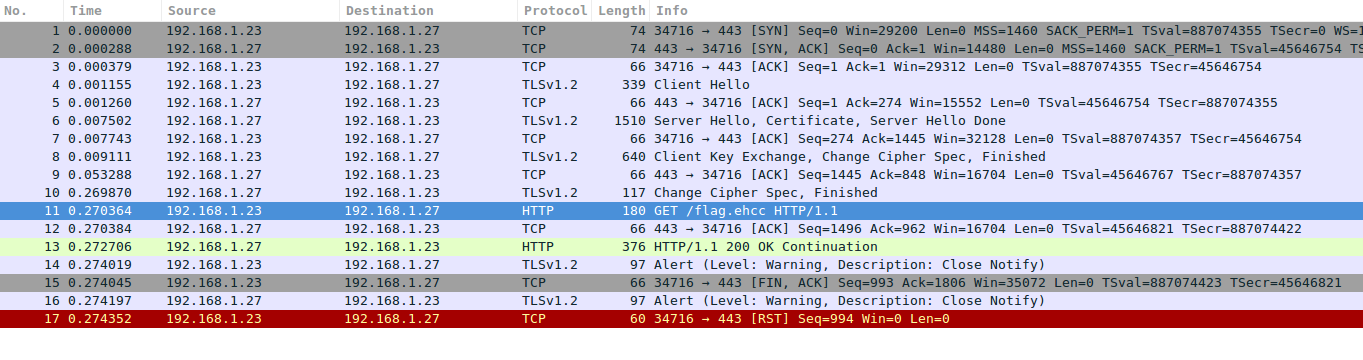
On fait “Appliquer” et la capture se déchiffre :
On obtient notre capture http en clair :
3.Comment se protéger
Il faut respecter les normes de sécurité et ne pas implémenter des algorithmes dépréciés comme le DES ou le 3DES.